我们必须清晰地认识到，0x0000000a 本身并不是一个“十进制数”，恰恰相反，前缀“0x”是一个明确的标志，告诉我们这是一个用十六进制（Hexadecimal）系统来表示的数字，这就像我们给一个单词加上引号，是为了说明它需要被特殊理解一样。“0x”就是在对计算机和懂行的人说：“我后面跟着的字符，要按照十六进制的规则来解读。”

这个十六进制数 0x0000000a 的“数学本质”究竟是什么呢？它的本质就是一个纯粹的数值，一个数学上的量，这个量本身是独立于任何进制表达方式的，我们可以用十进制来表示它，用二进制来表示它，甚至用八进制来表示它，但这个量本身是不变的，这就像“一只猫”，你可以用中文叫它“猫”，用英文叫它“cat”，用喵喵声来呼唤它，但那只猫本身并没有改变，0x0000000a 就是这个“猫”，而十六进制、十进制、二进制等等，只是呼唤它的不同“语言”。

我们来看看这个“名字”是怎么描述这只“猫”的，十六进制是一种“逢十六进一”的计数系统，它需要16个不同的符号来表示从0到15的数值，所以它借用了0-9这十个阿拉伯数字，然后加上A-F（或a-f）这六个英文字母,分别代表10到15。

我们来拆解 0x0000000a：

• 0x： 前缀,十六进制标识符。
• 0000000a： 这是数值的主体，前面的七个“0”是占位符，就像我们写十进制数“00010”时，前面的零只是为了格式对齐，并不改变数值大小，其核心是最后一位的“a”。
• a： 在十六进制中，这个字符代表十进制的“10”。

0x0000000a 的数学含义就是：在十六进制系统下，它表示的是数值“十”（十进制意义上的10），前面的零表示这个数占用了32位二进制数的存储空间（每个十六进制位对应4个二进制位，8个十六进制位就是32位），但数值上等同于简单的 0xa。

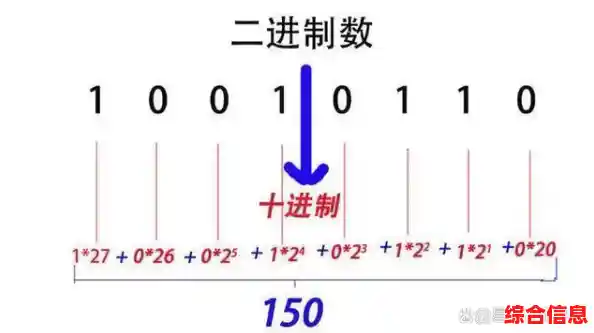
我们深入到最核心的进制转换原理，为什么“a”就等于“10”呢？这背后的原理是位权展开法，任何一种进位制数，其数值都等于每一位上的“数码”乘以该位的“位权”之后的总和。

• 位权：简单说就是“基数的次方”，对于十进制，基数是10，个位的位权是10^0=1，十位是10^1=10，百位是10^2=100，对于十六进制,基数是16。

我们把 0x0000000a 按照位权展开（从右向左，最右边是第0位）：

• 最右边一位是 a，也就是10，它所在的位置是第0位，位权是 16^0 = 1。
• 它左边的七位都是0，无论位权多大,0乘以任何数都是0。

这个数的数值 = (0 × 16^7) + (0 × 16^6) + ... + (0 × 16^1) + (10 × 16^0) = 0 + 0 + ... + 0 + (10 × 1) = 10。

通过位权展开，我们成功地将十六进制数转换成了我们最熟悉的十进制数，这个过程揭示了不同进制之间转换的通用法则：找到每个数码，确定其位权,然后求和。

在计算机科学中，十六进制和二进制的关系更为直接和深刻，十六进制之所以如此重要，根本原因在于它是二进制的“高度压缩版”，因为16是2的4次方（16=2^4）,所以一位十六进制数可以完美地对应四位二进制数。

让我们把 0x0000000a 转换成二进制,这个过程非常直观：

• a 在十六进制中代表10。
• 10 用四位二进制表示是多少？我们想，四位二进制能表示的最大数是15（1111），10落在其中，10 = 8 + 2，对应的二进制位是：8（2^3）的位置为1，4（2^2）的位置为0，2（2^1）的位置为1，1（2^0）的位置为0，所以是 1010。
• 前面的七个0，每个0在十六进制中代表0，而0用四位二进制表示就是 0000。

0x0000000a 的完整32位二进制表示就是：00000000 00000000 00000000 00001010，我们可以看到，最后四位 1010 直接对应着十六进制的 a，这种一目了然的对应关系，使得程序员在查看内存地址、数据包或机器码时,能够极其快速地在二进制和更简洁易读的十六进制之间进行心理转换。

0x0000000a 的数学本质就是抽象的数值“十”，它的十六进制表达“a”通过位权展开原理与十进制“10”等价，而其更深层的价值体现在与二进制的亲密关系中，它作为一个高效的“缩写工具”，将冗长的二进制序列变得清晰可读，从而让我们能更直观地理解计算机底层数据的真实样貌，它就像一座桥梁,连接着人类习惯的抽象数学世界和计算机运行的物理开关世界。